출처
en.wikipedia.org/wiki/Convolution
Convolution - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Binary mathematical operation on functions In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions (f and g) that produces a third
en.wikipedia.org
colah.github.io/posts/2014-07-Understanding-Convolutions/
Understanding Convolutions - colah's blog
In a previous post, we built up an understanding of convolutional neural networks, without referring to any significant mathematics. To go further, however, we need to understand convolutions. If we just wanted to understand convolutional neural networks,
colah.github.io
멋진 글이 하나 있길래 느낌을 잊지 않으려고 써본다.

합성곱 하는법. 두 함수 중 아무 함수를 고르고 반전 후 음의 무한대부터 양의 무한대까지 선택한 함수를 이동시키면서 두 함수의 곱의 적분값을 계산한다. (검은 선)
참 쉽죠?
공 떨어뜨리기로 알아보는 convolution
공을 공중에서 낙하시켰을 때, 공이 a만큼 떨어진 곳에 착지할 확률을 f(a)라고 하자. 그 첫 착륙지점에서 공을 들어올려 또 다시 낙하시켰을 때, 그 자리에서 b만큼 떨어진 곳에 착지할 확률을 g(b)라고 한다. (공을 들어올린 높이가 달라지면 확률도 달라지니까 f와 g가 구별된다.)

그러니 이 사건이 일어날 확률은 f(a)g(b)이다. a+b = c 로 변수를 정하고 c = 3인 상황을 가정하면 두 번의 낙하를 통해 c=3에 도달할 경우의 수는 많다. f(1)g(2) 일 수도, f(0)g(3)일 수도 있다. c에 도달하는 모든 경우의 수를 합한 확률은


그럼 이게 합성곱이랜다. (이산변수를 연속변수로 바꿔주면 ∑가 ∫ 이 되니까 정의대로 적분 맞지요?) 여기서 b = c-a로 치환하면,

이걸 공으로 이미지화 하면

convolution 시각화
공이 어느 지점에서 낙하해서 출발점에서 x만큼 거리가 있는 곳에 착륙할 확률이 f(x)면, 착지한 곳으로부터 x만큼 거리가 있는 곳에서 떨어지기 시작했을 확률은 f(-x)이다.
- 왜 f(-x)인지..
낙하 시작점을 X, 착지점을 Y라고 했을 때, X~Unif(-L,+L)인 확률변수이고 Y=0이라고 가정하고 P(X=x | Y=0)이 정말로 f(-x)인지 증명하면 된다.
베이즈 룰에 따라 P(X=x | Y=0) = P(Y=0 | X=x)P(X=x) / P(Y=0) --- (1)
그리고 착지지점이 0일 확률 P(Y=0) = ∑ {x' in S} ( P(X=-x')f(x') ) (여기서 S=[-L, +L]) --- (2)
X는 유니폼이니까, P(X=x) = P(X=-x') = p를 (2)에 대입하면 P(Y=0) = p * ∑ {x' in S} f(x') = p * 1. (왜냐면 f( )는 확률변수인데 모든 정의역?을 훑어 합하니까 1)
또한 식 (1)에서 P(X=x) = p 이고 P(Y=0 | X=x) = f(-x)이므로 P(X=x | Y=0) = f(-x) 성립.

만약 내가 두번 낙하 후에 위치 c에 착지할 것을 알고있다면, 그 이전 위치(첫 착지 지점)이 a일 확률은?

방금 위에서 말한대로 g(-(a-c)) = g(c-a). 근데 여기서 가능한 a의 경우의 수는 [-L, +L] 에 다 있다.

그 경우의 수를 따르는 확률을 다 곱하면 맨 처음 말한 합성곱이랑 똑같지롱

졸라 신기하다 그림 3은 두번째 착지지점에 관한 거였고 그림 6은 첫번째 착지지점에 관한 건데 둘이 같아벌임 ㅇㅁㅇ!
최종 위치 c를 옮기면서 보면 합성곱 느낌이 좀 더 오는데
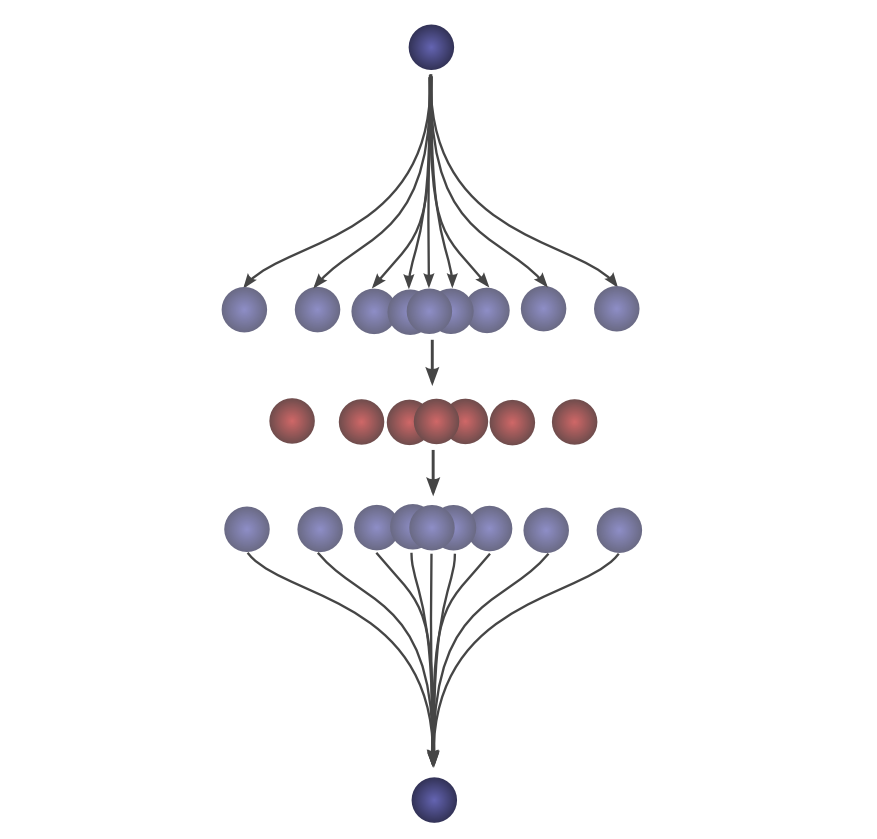
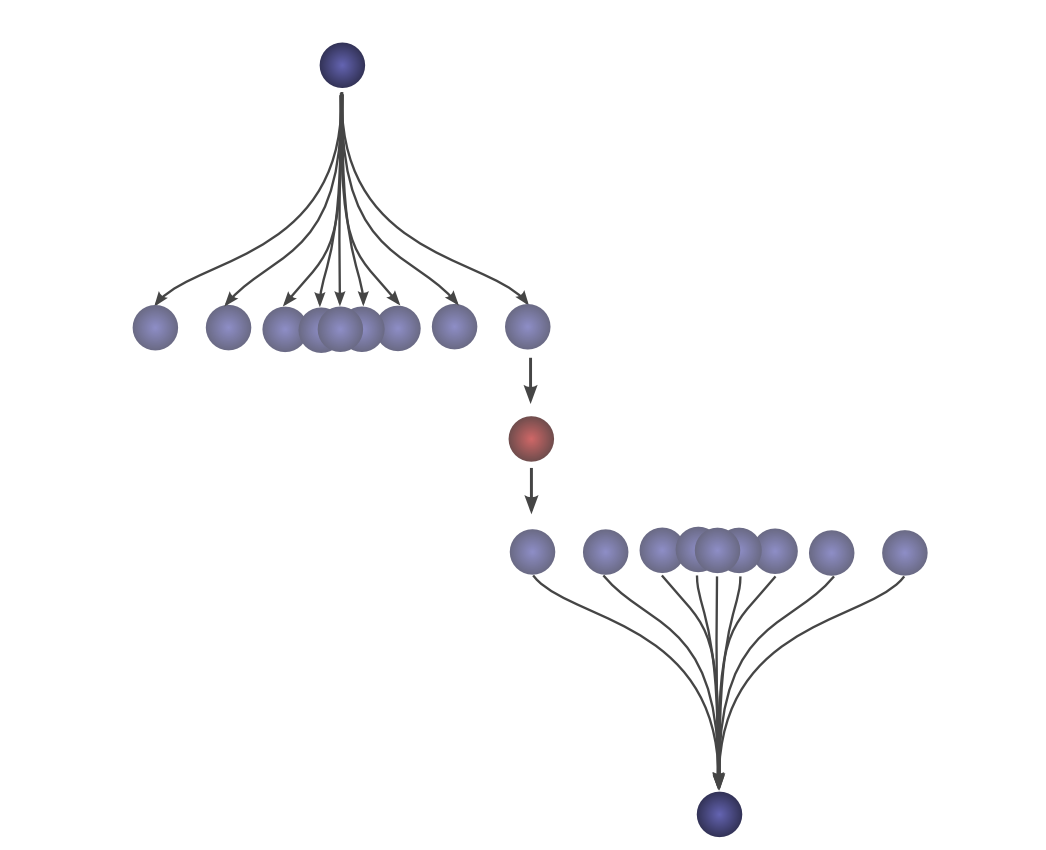
그림 7처럼 첫 낙하지점과 최종 착지지점이 같으면 (a=c 이면) 합성곱 (f*g)(c)의 값이 최대일 것이고 멀어질 수록 합성곱도 작아진다. 그림 8은 f와 g가 둘 다 정규분포인 pdf 라고 보면 타당한거 같고 이쯤오면 위키에 있는 움짤도 보면 완전 이해됨.

더 높은 차원의 convolution
이제 공이 3차원 공간에 있다고 생각해보자.

이제 a,b,c는 스칼라가 아닌 벡터로 표현된다.


그림9 에서 한 함수가 1차원 상에서 움직이며 다른 함수를 훑고 지나가며 합성곱 결과를 뽑아낸 것 그대로 2차원으로 옮겨본다면,

어디서 많이 본 이 그림이 좀 다르게 보일 것이다. 그림 9의 검은선이 output, input이 파란함수, kernel을 빨간함수로 보자.
댓글