지수분포는 이산분포인 기하함수와 비슷한 연속분포이다. 사건이 서로 독립적일 때, 일정 시간동안 발생하는 사건의 횟수가 푸아송 분포를 따른다면, 다음 사건이 일어날 때까지 대기 시간은 지수분포를 따른다
interval time t 에서의 평균 성공확률은 tλ이다.
연속확률변수 X가 지수분포를 가진다면 (λ>0), PDF는 다음과 같다.
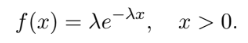
이때 X ~ Expo(λ)라고 표기하며 상응하는 CDF는

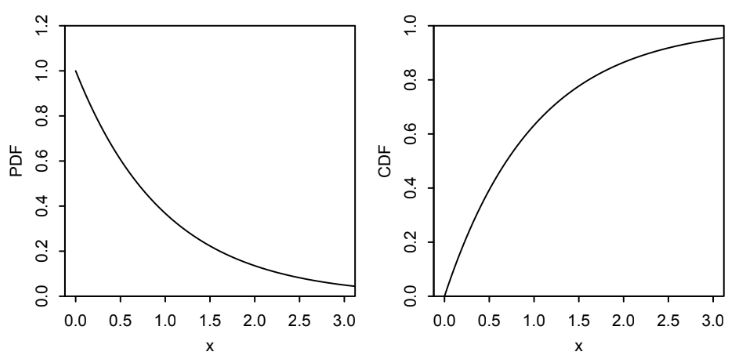
위 그림은 X~Expo(1)의 PDF와 CDF를 그린 것이다.
여기서 우리는 X를 가지고 scale을 조정하여 일반적인 Expo(λ)를 유도할 수 있는데,

위와 같이 X를 원하는 λ값으로 나누면 그 확률변수는 Expo(λ)를 따르게 된다.

간단한 부분적분을 실행하면 위와 같이 지수분포의 기댓값과 분산을 구할 수 있다.
Memoryless property
지수분포는 망각성질이라는 아주 특별한 특성을 가지고 있는데,
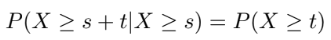
(s, t >0)
아주 간단한 식이라 직관적으로 의미를 알 수 있다. 어떤 사건이 일어나길 s만큼의 시간을 보냈어도, 거기서 t만큼의 시간을 더 보내야할 확률이 그냥 처음부터 t만큼 기다릴 확률과 같다!
조건부확률의 정의를 활용해 간단하게 증명이 가능하다.

지수분포와 기하분포의 관계

unit time을 N개의 subinterval로 나누고 각 subinterval마다의 사건이 일어날 확률이 i.i.d. Bern(p)라고 가정하자.
λ를 한 unit time동안 일어나는 사건 수의 평균이라고 한다면, λ=Np이다.
사건이 일어나기까지의 subinterval의 수 G는 기하분포를 따른다.
여기서 G가 k보다 클 확률(사건이 일어나기까지 k번의 시도 이상일 확률) CDF는 다음과 같다.

여기서 사건이 일어나기까지의 시간 개념 t를 도입하자면, t=k/N이다. (위 그림 참고)
이 때, N을 무한대로 근사한다면 subinterval이 무한히 작아지면서 본디 시간의 성질처럼 연속적인 시간 상에서 논의를 진행할 수 있다. (위 그림 상의 간격 수가 무한히 늘어나면서 한 간격의 길이는 매우 작아짐)
이제 사건이 일어나기까지의 시간을 확률변수 X로 놓고 이것이 t보다 클 확률은 다음과 같고,

지수분포의 CDF와 기하분포의 CDF가 극한으로 연결되어 있음을 확인할 수 있다.
'수학 > 확률' 카테고리의 다른 글
| Multivariate Normal (0) | 2019.11.17 |
|---|---|
| Covariance & Correlation (0) | 2019.11.17 |
| Moments & MGF (0) | 2019.11.10 |
| Normal Distribution (0) | 2019.11.10 |
| Uniform Distribution (1) | 2019.11.09 |




댓글